On Trivalue Oddagons

One of my friend groups has been getting into Sudoku recently. Sudoku sort of reminds me of Minesweeper in the sense that a lot of the work comes from discovering logical implication chains to prove the existence/nonexistence of a number. I’ve been going through some strategies on this Sudoku campaign which is nice for formalizing the strategies that one typically derives when playing Sudoku (i.e. “Hidden Singles”, “Naked Pairs”, etc.).

Yesterday I was made aware of this one pattern called the trivalue oddagon (also known as Thor’s Hammer, shortened as tridagon) which supposedly is this sort of gimmick pattern that artifically inflates the computer-analyzed difficulty of puzzles. I would imagine it has to do with how this pattern cannot be directly solved on a computer with anything short of bruteforce searches to analyze this pattern. Interestingly, because of its distinctiveness, it’s not too difficult to spot by a human, though my understanding is that it doesn’t come up in puzzles very often at all. Here’s how it looks, courtesy of my friend Karo:

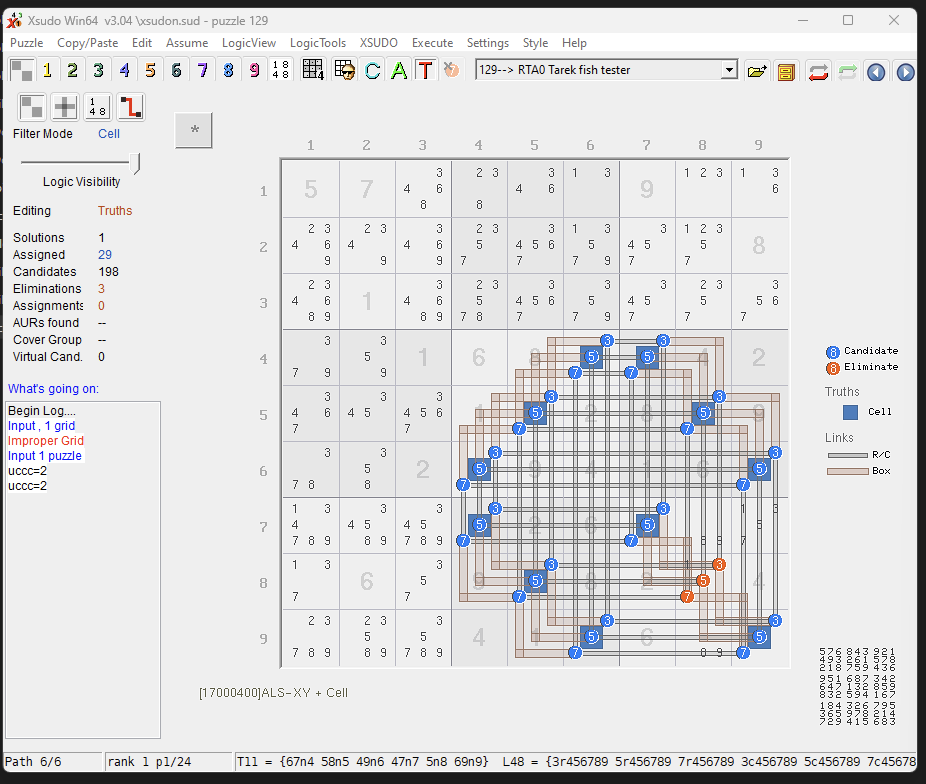
The next step in this puzzle is to deduce that the cell in Row 8 Col 9 (candidates marked \(\{1,3,5,7\}\)) must be a \(1\), because if it were not, this structure (i.e., assigning 3, 5, 7 in these four boxes) would not be possible.

This logic is not very clear to me, so I’ve attempted to prove it below. To do this, we’ll first describe a set of patterns on the Sudoku board that can be represented as a subgraph \(G\). Then, we shall show that \(G\) is not \(4\)-colorable.

Formalizing the Trivalue Oddagon Board State

Consider four boxes, WLOG contiguous. Name these boxes \(A,B,C,D\) in row-major order. We’ll also assume that the three numbers remaining are \(\{1,2,3\}\). Clearly, each box contains a permutation of \(\{1,2,3\}\).

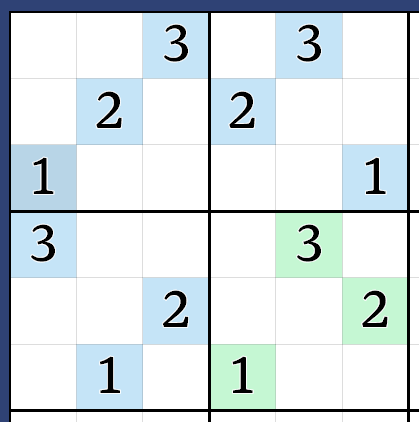
Here, the number represents the row (from bottom to top, i.e. with the intuition that the numbers are “ascending”) within its box. We can read each box left-to-right. Hence, the permutations above, described in row-major order, would be \(A=(1,2,3), B=(2,3,1), C=(3,1,2), D=(1,3,2)\).

Furthermore note the parity of the permutation, \(\sigma\), which is the parity of the number of inversions of each element. There are \(0,2,2,1\) inversions respectively, so the parities are \(0,0,0,1\).

Note that the parity of each element corresponds to exactly whether or not the box is increasing left-to-right (i.e. wraps up and to the right). If it is even, it is ascending; if it is odd, the element is descending.

Hence, the claim is this: if exactly three of \(\{A,B,C,D\}\) are ascending or exactly three are descending, there exists no possible numbering/coloring of this structure.

First, we wish to show a lemma; every odd permutation in \(S_3\) has exactly one fixed point. To see this, the odd permutations in \(S_3\) are precisely the three transpositions: \((1,2)\), \((1,3)\), and \((2,3)\). Each transposition swaps two elements while leaving the third fixed. Thus, every odd permutation in \(S_3\) has exactly one fixed point.

Now, consider the parity of \(A\circ B\circ C\circ D\). If it is odd, there is exactly one fixed point.

If exactly three of \(\{A,B,C,D\}\) are ascending or exactly three are descending, we see that \(A\circ B\circ C\circ D\) is also odd. Thus, there exists exactly one fixed point.

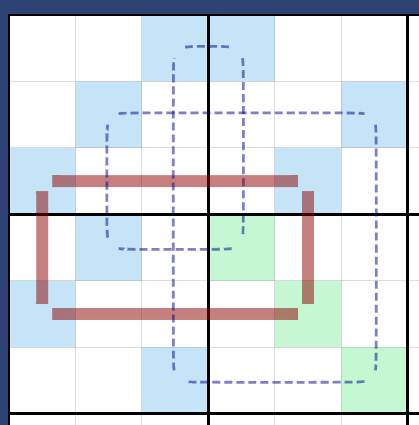
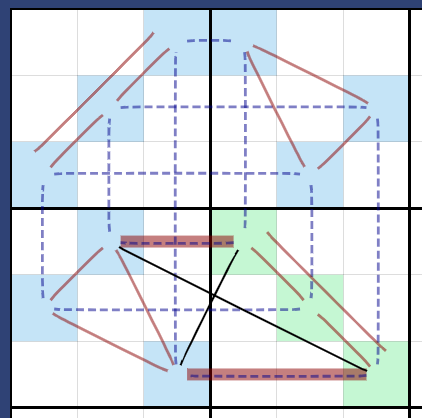
Here, observe that the permutations of three even and one odd element produces exactly one fixed point, highlighted as the red rectangle. Furthermore, note that the other two points are not fixed. Hence, they cannot form an square, so it must be an \(8\)-cycle, highlighted in the purple dotted lines.

This turns out to be exactly what we need to represent it as a graph.

Graph Representation

The Sudoku is a famous instance of coloring problem in graph theory. Vertices are the cells of the Sudoku, and edges occur between two vertices if and only if the two cells cannot be the same number. Hence, we wish to represent the trivalue oddagon as a graph.

In each box, the three cells may never be the same number, so they form a complete graph with \(3\) vertices (i.e. a \(K_3=C_3\)).

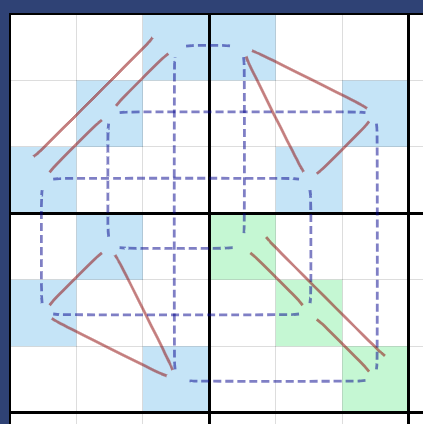
Consider this graph as an example. This graph is messy, but we can represent it more nicely be describing it as the isomorphism of a more well-defined graph. Specifically, consider how it is exactly one edge swap away from \(C_3\square C_4\), i.e. the cartesian product. To see the edge swap, swap the edges as shown below, deleting the dotted lines highlighted in red and adding the lines in black. The vertices affected in the swap are always the two vertices that are not fixed.

This amounts to \(C_3\square C_4\) exactly; it’s left as an exercise to the reader to double check the isomorphism if needed.

Let \(G=C_3\square C_4\) and \(G'\) be an edge-swapped \(G\), which we will rigorously define later. While the chromatic number \(\chi(G)=3\), it turns out that \(\chi(G')=4\), which is the reason why the trivalue oddagon structure cannot be possible with three numbers.

To show this, we wish to label the vertices of \(G'\). Let \((a,b)\) be the vertex in \(G'\) such that it is the \(a\)th vertex in \(C_3\) and the \(b\)th vertex in \(C_4\). Hence, \(a\in[0,2], b\in[0,3]\). Thus, by definition of a Cartesian product,

We also define \(G'\) by swapping edges \(((0,0),(3,1))\) and \(((0,1),(3,0))\), such that the new edges are \(((0,0),(3,0)),((0,1),(3,1))\). Then we wish to show \(\chi(G')> 3\).

Lower-bounding \(\chi(G')\)

To do this, we introduce a graph theoretic intuition of “coloring parity” on each \(C_3\). Each \(C_3\) must be colored with three numbers (say, \(\{1,2,3\}\)).

Then for a 3-coloring \(f: \{(a,0), (a,1), (a,2)\} \to \{1,2,3\}\) of the \(a\)-th copy of \(C_3\) in \(G'\), we say the coloring is ascending if \(f(a,i) \equiv f(a,0) + i \pmod{3}\) for all \(i \in \{0,1,2\}\). Otherwise, we say it is descending.

Note that any valid 3-coloring of \(C_3\) must be either ascending or descending, which forces the coloring to be a cyclic permutation in one direction or the other.

Now, consider the \(0\)th and \(1\)st \(C_3\). We claim they must have the same parity. Suppose for contradiction that the \(0\)th is ascending with \(f(0,i) = c + i\) (mod 3) and the \(1\)st is descending.

In \(G'\), the adjacencies between these copies are (unchanged from \(G\)):

• \(((0,0), (1,0))\), so \(f(1,0) \neq c\)
• \(((0,1), (1,1))\), so \(f(1,1) \neq c + 1\)
• \(((0,2), (1,2))\), so \(f(1,2) \neq c + 2\)

For the \(1\)st \(C_3\) to be descending with \(f(1,i) = f(1,0) - i\) (mod 3):

• If \(f(1,0) = c + 1\): then \(f(1,1) = c\), contradicting \(f(1,1) \neq c + 1\)
• If \(f(1,0) = c + 2\): then \(f(1,1) = c + 1\), contradicting \(f(1,1) \neq c + 1\)

Therefore, adjacent \(C_3\) copies must have the same parity. By the same argument, all four \(C_3\) copies in the unmodified portion of \(G\) must have the same parity.

Now, consider the edges between the \(0\)th and the \(3\)rd \(C_3\), which has been edge swapped. With the swapped edges \(((0,0),(3,1))\) and \(((0,1), (3,0))\), if both are ascending, we see \(f(3,0) \neq f(0,1) = c+1\), so \(f(3,0) \in \{c, c+2\}\).

Consider the case \(f(3,0)=c\), \(f(3,2)=c+2=f(0,2)\), a contradiction. Furthermore consider the case \(f(3,0)=c+2\); then \(f(3,1)=c+0=f(0,0)\), a contradiction. WLOG we can see that this coloring is not possible if both are descending. Hence, the \(0\)th and the \(3\)rd \(C_3\) must not share the same parity.

This is a contradiction, as we have shown \(0\)th and the \(3\)rd \(C_3\) have the same parity above. Thus, \(\chi(G')\not\leq 3\). This shows that any trivalue oddagon cannot be filled with \(3\) numbers, and we are done.

Applying the Trivalue Oddagon

Consider the example described earlier:

Here, consider the cell in Row 8 Col 9. Suppose for contradiction it isn’t \(1\). Since we have shown this trivalue oddagon not to be three-colorable, we have a contradiction immediately, and we can conclude that cell must be a \(1\).